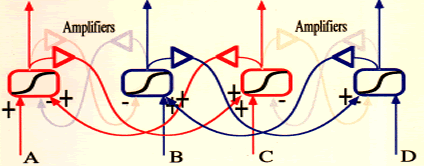

This diagram shows two flip-flops. A and B form one, C and D the other. But these flip-flops are interconnected so that A and C, and B and D separately support each other in the sense that if the A output is high it delivers a positive input to help C go high and vice-versa. Similarly for B and D. We assume that these associative coupling constants are small enough that it is possible for A to be high while C stays low, and vice-versa. Otherwise, there might as well be only one flip-flop, either AB or CD. With a small associative coupling constant, if A is high, it takes a smaller input at C to switch the CD flip-flop into the C-high condition than would be the case if B was high and A low.
The connections between A and C, and between B and D, are positive feedback loops. If the coupling constants are too high, the loop gain can go above unity, forcing the whole system into a locked up condition. However, this positive feedback loop is mitigated by the negative loops ACDBA and ABDCA. The whole analysis is complex, but certain aspects are easily seen.
Firstly, we assume that the associative coupling constants are small. What happens then is that if the input to the AB flip-flop is such that the A output is high (A is "seen"), then it is easier to "see C" than it is to "see D." A is "associated" with C, and B with D. One can readily understand this as a simplification of what may happen in everyday "association," and in particular as a kind of labelling, in which seeing A allows the label "C" to be perceived. We will not pursue this further here, but to see the implications, imagine a forest of elements coupled positively and negatively, with relatively low coupling constants, rather than, as here, having two pairs of positively coupled and two pairs of negatively coupled elements. Such an arrangement would show clusters of associations and clusters of mutually inhibitory elements. Think "spin glass."
The issue of interest at this point is simply to illustrate phase transitions and the effects of changing coupling constants. The spin glass effect among coupled perceptual functions will not be pursued, but it could be important in a discussion of control theory in the use of language, among many related psychological phenomena.
Next we examine coupling in the form of catalysis, following Kauffman, to illustrate the effects that can occur when a low-probability phenomenon can occur in large groups of interacting entities..